고정 헤더 영역
상세 컨텐츠
본문
정렬 알고리즘은 일반적으로 비교 정렬을 하는데, 각 원소의 값을 비교하지 않고 정렬하여 시간복잡도를 O(N)으로 줄이는 특수한 정렬 알고리즘이 존재한다. 그 중 하나가 계수 정렬 (Counting Sort)이다. 추가로 정렬을 하기 위해서 각 원소의 값을 최소 1번씩은 확인해야 하므로 정렬 알고리즘이 O(N)보다 시간 복잡도는 낮아질 수 없다는 것은 자명하다.
Counting Sort는 정렬하고자 하는 값의 범위가 O(N)을 넘지 않는 경우 사용할 수 있다. 예를 들어 k 이하의 자연수가 될 수 있고, 실수라고 한다면 수의 범위가 무한해지기 때문에 사용할 수 없다. Counting Sort의 동작 원리는 말 그대로 값을 세서 개수를 기록해둔 뒤 나중에 순서대로 데이터를 배치하는 것이다. 도식을 통해 이해해보자.
데이터의 범위가 0 이상 10 이하의 정수인 어떤 숫자들을 counting sort로 정렬하려고 한다. 정렬하고자 하는 배열을 A라고 하자.

이 경우 0부터 10까지 데이터가 몇 번 나오는 지 세서 기록해 둘 배열이 필요한데, 이를 B라고 하자. B의 i 번째 값은 A에 i가 나온 횟수를 의미한다.

이제 2가 2개, 4가 1개, 5가 2개, 7이 2개, 8이 2개, 10이 1개 인것을 알았으므로, 순서대로 2, 2, 4, 5, 5, 7, 7, 8, 8, 10으로 정렬할 수 있게 된다. 이러한 과정은 배열 A의 원소들을 하나씩 살펴보며 개수를 기록하고, 배열 B를 살펴보며 원소의 개수별로 배치하는 과정이므로 시간 복잡도는 O(N)에 해당한다.
여기서 추가적인 과정을 거쳐서 A에서 값이 동일한 원소들에 대해 배치되었던 순서를 그대로 유지하면서 정렬할 수도 있다. 위에서는 단순히 숫자를 정렬하는 과정이었지만, 예를 들어 나이와 이름으로 구성된 데이터를 나이 순으로 정렬하고자 할 때, 기존의 순서를 최대한 유지하면서 나이를 기준으로 정렬하고 싶을 수 있다. 이렇게 기존 순서를 최대한 유지하면서 정렬하는 것을 Stable Sort라고 한다. Stable Sort가 가능한 정렬로 Merge Sort가 있다. Merge 과정에서 기존의 순서를 유지하도록 하면 되기 때문이다.
Counting Sort에서 Stable하게 정렬하기 위해서는, 추가 배열 C가 필요하다. 배열 C는 배열 B에서 값을 차례로 누적해서 기록한 배열이다. 위 B에서 C를 만들면 아래와 같이 만들어 진다. i = 0, ... , 10에 대해서 C[i] = B[0] + B[1] + ... + B[i]인 것을 확인할 수 있다. 이렇게 누적을 한 이유는, 각 값이 정렬된 후 배치될 인덱스를 계산하기 위해서이다. 예를 들어, 10은 정렬 이후 인덱스 9에 배치된다.

Stable하게 정렬하기 위해서, A의 원소를 뒤에서부터 하나씩 보면서 배치할 것이다.
(1) A에서 맨 뒤의 원소 10을 배치하기 위해 C[10]을 보면 값이 9이므로, 결과 배열의 10번째 index에 배치한다. 그리고, C[10]의 값을 1 빼준다.
(2) 그 다음 원소 7을 배치하기 위해 C[7]을 보면 값이 6이므로, 결과 배열의 7번째 index에 배치하고 C[7]의 값을 -1 해준다.
(3) 그 다음 원소 8을 배치하기 위해 C[8]을 보면 값이 8이므로, 결과 배열의 9번째 index에 배치하고 C[8]의 값을 -1 해준다.
(4) 그 다음 원소 7을 배치하기 위해 C[7]을 보면 값이 5이므로, 결과 배열의 6번째 index에 배치하고 C[7]의 값을 -1 해준다.
(5) 그 다음 원소 2를 배치하기 위해 C[2]를 보면 값이 2이므로, 결과 배열의 2번째 index에 배치하고 C[2]의 값을 -1 해준다.
(6) 그 다음 원소 5를 배치하기 위해 C[5]를 보면 값이 5이므로, 결과 배열의 5번째 index에 배치하고 C[5]의 값을 -1 해준다.
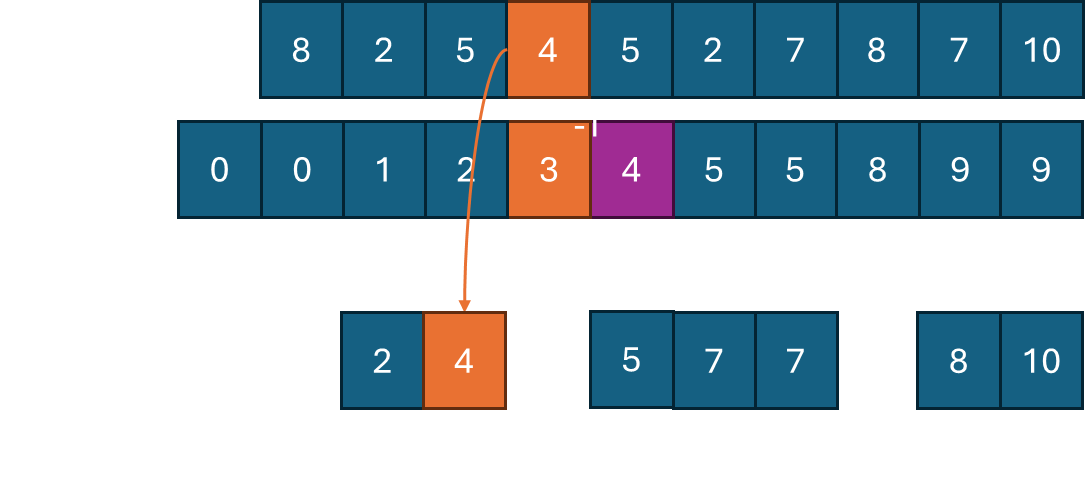
(7) 그 다음 원소 4를 배치하기 위해 C[4]를 보면 값이 3이므로, 결과 배열의 3번째 index에 배치하고 C[4]의 값을 -1 해준다.
(8) 그 다음 원소 5를 배치하기 위해 C[5]를 보면 값이 4이므로, 결과 배열의 4번째 index에 배치하고 C[5]의 값을 -1 해준다.
(9) 그 다음 원소 2를 배치하기 위해 C[2]를 보면 값이 1이므로, 결과 배열의 1번째 index에 배치하고 C[2]의 값을 -1 해준다.
(10) 그 다음 원소 8를 배치하기 위해 C[8]를 보면 값이 8이므로, 결과 배열의 8번째 index에 배치하고 C[8]의 값을 -1 해준다.








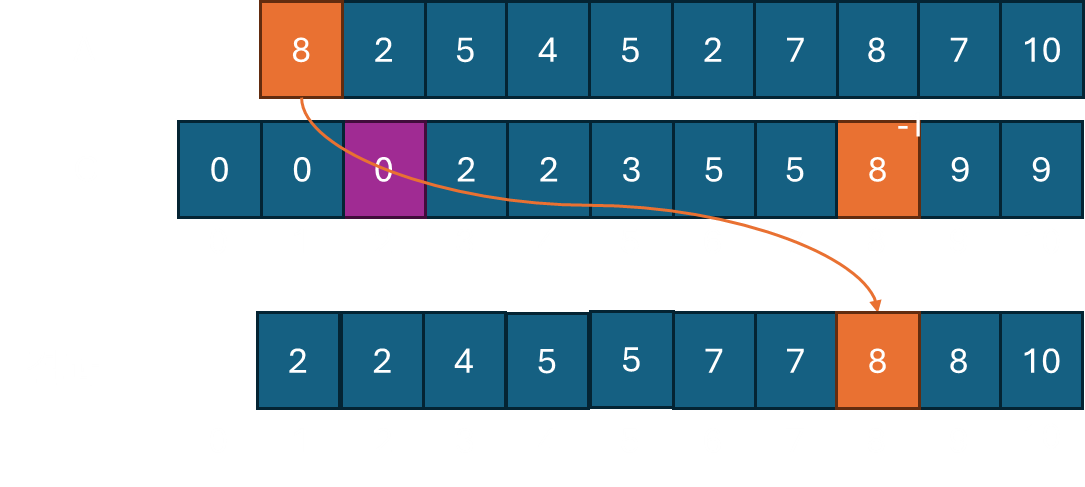
이렇게 하면 counting sort 과정에서 stable하고 정렬을 할 수 있게 된다. 추가 과정은 B 배열에서 하나씩 살펴보면서 누적해서 C 배열을 만드는 과정 O(N), A를 거꾸로 하나씩 살펴보면서 결과 배열에 배치하는 과정 O(N)으로 마찬가지로 O(N)의 시간 복잡도를 갖게 된다. 알고리즘 문제를 풀 때 입력 데이터의 형태를 잘 살펴보고, O(N)의 stable sort를 사용하는 경우 유용하게 사용할 수 있다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 정렬 - 힙 정렬, O(NlogN) (0) | 2024.03.17 |
|---|---|
| [알고리즘] 정렬 - 퀵 정렬, O(NlogN) (0) | 2024.03.17 |
| [알고리즘] 정렬 - 병합 정렬, O(NlogN) (0) | 2024.03.17 |
| [알고리즘] 정렬 - 삽입 정렬, O(N^2) (0) | 2024.03.17 |
| [알고리즘] 정렬 - 버블 정렬, O(N^2) (0) | 2024.03.17 |




