고정 헤더 영역
상세 컨텐츠
본문
24.03.20 수정 - 처음에 데이터 전체를 힙 구조로 만드는 과정이 O(NlogN)이라고 상한을 과하게 잡아서 작성했는데, 실제로는 Θ(N)의 시간 안에 해결된다. 증명과정을 추가하여 작성했다.
힙 정렬은 힙(Heap)이라는 자료구조를 이용해 정렬하는 방식이므로 우선 힙에 대해 이해할 필요가 있다. 다음은 Heap의 조건이다.
Heap이란?
1. 완전 이진 트리이다. 모든 경로의 가장 아래층을 제외하고는 모두 채워져있다.
2. 왼쪽부터 노드가 채워진다.
3. 부모 노드의 값이 자식 노드의 값보다 항상 작다(크다).
Heap은 3번 조건에 따라 MaxHeap와 MinHeap으로 나뉜다. 부모 노드의 값이 자식 노드의 값보다 작으면 MinHeap, 크면 MaxHeap이다. 보통 MaxHeap을 사용하는 것 같지만 나는 MinHeap으로 공부해서 MinHeap을 사용할 예정이다.

완전 이진트리를 실제로 노드를 잇는 형식으로 구현하지 않고, 일대일로 대응되는 배열로 생각할 수 있는 방식이 있는데, 트리의 맨 위층부터 차례대로 좌측에서 우측으로 가는 순서대로 배열에 저장하는 방법이다. 이 경우 i 번째 원소의 왼쪽 자식은 2*i번째, 오른쪽 자식은 2*i+1번째 노드이다. 다만 이는 1부터 세는 방식으로 했을 때 경우이고, 배열 인덱스처럼 0부터 센다고 한다면 인덱스 i의 왼쪽 자식 인덱스는 2*i+1, 오른쪽 자식 인덱스는 2*i+2이다.

힙 정렬 (Heap Sort) 소개
MinHeap을 이용한 힙 정렬은 루트가 최소값이기 때문에 루트의 값을 뽑고, 루트를 제외한 트리를 힙의 성질에 맞게 다시 힙 구조로 만든 뒤, 루트 값을 뽑는 과정을 반복하면서 최소값부터 차례대로 정렬하는 알고리즘이다. 힙 정렬 과정에서 루트를 뽑는 과정은 단순히 인덱스 접근이므로 상수 시간이 걸리는 간단한 작업이다. 따라서 Heap 정렬에서 중요한 부분은 Heap 구조를 만드는 Heapify 과정이라고 할 수 있다.
Heapify 과정에 대해 알아보자. 우선 힙을 배열로 다룬다면 배열의 0번째 인덱스부터 차례대로 값을 넣는다면 힙의 조건 1, 2는 자연스럽게 만족하는 것으로 생각할 수 있다. 우리가 신경써야 할 조건은 3번 조건이다. 부모 노드의 값이 자식 노드의 값보다 작아야 한다는 사실도 알고, 힙과 대응되는 배열을 다룰 때 부모 노드와 자식 노드의 인덱스 관계를 알고 있기 때문에 이를 이용해서 원소의 순서를 변경하여 힙 구조를 만족시키도록 할 수 있다.
3번 조건을 만족시키기 위해 고려해야 할 노드는 자식이 있는 노드이다. 따라서 먼저 자식 노드가 있는 노드를 추려내야 한다. 위 그림에서 10개의 원소를 가진 완전 이진트리에서 자식이 있는 노드는 1번~5번 노드로 총 5가지이다. 여기서 1개의 원소를 더 뺀, 9개의 원소를 가진 완전 이진트리는 10번 원소가 빠진 형태이므로 자식이 있는 노드는 1번~4번 노드로 총 4가지이다. 여기서 1개의 원소를 더 뺀 이진트리는 1번~4번 노드만 자식을 가진다. 여기서 규칙성을 찾을 수 있는데, 원소의 개수가 N개인 완전 이진트리에서 자식이 있는 노드의 개수는 ⌊N/2⌋개라는 사실이다. 노드 번호로 따지면 1~⌊N/2⌋번 노드이고, 인덱스로 따지면 0~⌊N/2⌋-1 의 원소이다.
자식이 있는 노드를 추려낸 후에는 각각의 노드에 대해, 자식의 값이 본인의 값보다 작다면 둘을 swap하는 과정을 거치면서 힙의 3번 조건을 만족시키도록 구조를 변경한다. 이 떄 본인과 자식을 swap 했으면, 자식 값이 변경되므로 자식노드와 자식노드의 자식노드의 관계에서 3번 성질을 만족시키지 못할 수도 있다 (자식 > 자식의 자식). 따라서 재귀적으로 heapify를 호출하며 내려가면서, 자식이 없는 노드까지 반복한다. heapify를 실행하고 나면 heapify를 실행한 노드 아래로는 모두 힙의 3번 성질을 만족하게 된다. 이러한 과정을 ⌊N/2⌋번째 노드 부터 1번째 노드까지 거꾸로 실행하면, 전체 데이터가 힙 구조를 만족하게 된다.
이렇게 데이터를 힙구조로 변경한 뒤, 루트 노드를 뽑아서 정렬한 결과를 저장할 배열의 첫번째에 저장한다. 그리고 루트노드와 가장 마지막 노드를 스왑한다. 이러면 힙구조의 성질이 깨지기 때문에 루트노드에 대해 heapify를 진행한다. 그러면 다시 전체적으로 힙 구조를 만족하게 되고, 다시 루트 노드가 최소값이 된다. 이러한 과정을 반복하면서 루트 노드에서 계속 최소값을 뽑아 작은 값부터 차례대로 정렬할 수 있게 된다.
이 과정을 간단하게 요약하자면 다음과 같다.
Heapify 과정 (x 노드에 대해, x 노드의 자식 : y, z)
1. y, z가 존재하지 않으면 return
2. y만 존재하고, y가 x보다 작으면 swap
3. y, z가 모두 존재하고, y, z 중 최소 값이 x보다 작으면 swap
- swap이 일어났으면 swap한 자식에 대해 Heapify를 재귀적으로 실행.
=> 결과, x노드 아래는 힙 성질을 만족
이러한 Heapify 과정을 ⌊N/2⌋번째 노드 부터 1번째 노드까지 거꾸로 실행하면 전체가 heap 구조를 만족한다.
이제 힙 정렬의 시간 복잡도를 계산해보자. 우선 무작위로 정렬되어있는 데이터를 힙구조를 만족하도록 바꿔야하므로, ⌊N/2⌋번째 노드 부터 1번째 노드까지 총 ⌊N/2⌋번 heapify가 일어난다. heapify는 swap이 계속 일어나면 최대 해당 노드를 루트로 하는 서브트리의 높이만큼 일어나므로, heapify의 시간복잡도는 O(logN)이라 할 수 있다. (상한의 의미를 강조해서 O를 사용했다). 이게 ⌊N/2⌋번 일어나므로 처음 데이터를 힙구조로 바꾸는 과정이 O(NlogN)의 시간이 소요된다.
[24.03.20] 내용 수정, 추가 - 처음 데이터를 힙 구조로 바꾸는 과정은 상한을 과하게 잡아서 O(NlogN)이라고 생각할 수도 있지만, 좀 더 엄밀히 계산하면 Θ(N)의 시간 안에 해결된다. 시간 복잡도 증명과정 중에 무한 등비급수를 활용하는 부분이 인상적이다. 이러한 부등식 증명과정에서 적분이 사용되는 경우는 좀 본 것 같은데 무한 등비급수를 적절히 식 변형해서 1/2가 활용되는 부분이 흥미롭다.

이후, 반복적으로 루트노드를 뽑고 루트노드에 heapify를 적용하는 과정의 시간복잡도를 계산해보자. 이 과정은 데이터의 개수만큼 반복되어야 하므로 N번 발생한다. 루트노드를 뽑아서 결과 배열에 저장하는 과정은 상수 시간이 걸리므로 총 O(N)이 소요된다. 루트노드를 뽑은 뒤, 마지막 노드와 스왑하고 heapify를 하므로 heapify 역시 N번 일어나고, 이는 O(NlogN)의 시간이 소요된다. 따라서 모든 과정을 다 합치면 O(NlogN)의 시간이 소요된다.
아래에 힙 정렬의 과정을 도식화 해보았다.
1. 무작위 정렬된 데이터를 힙구조로 만든다. O(NlogN)




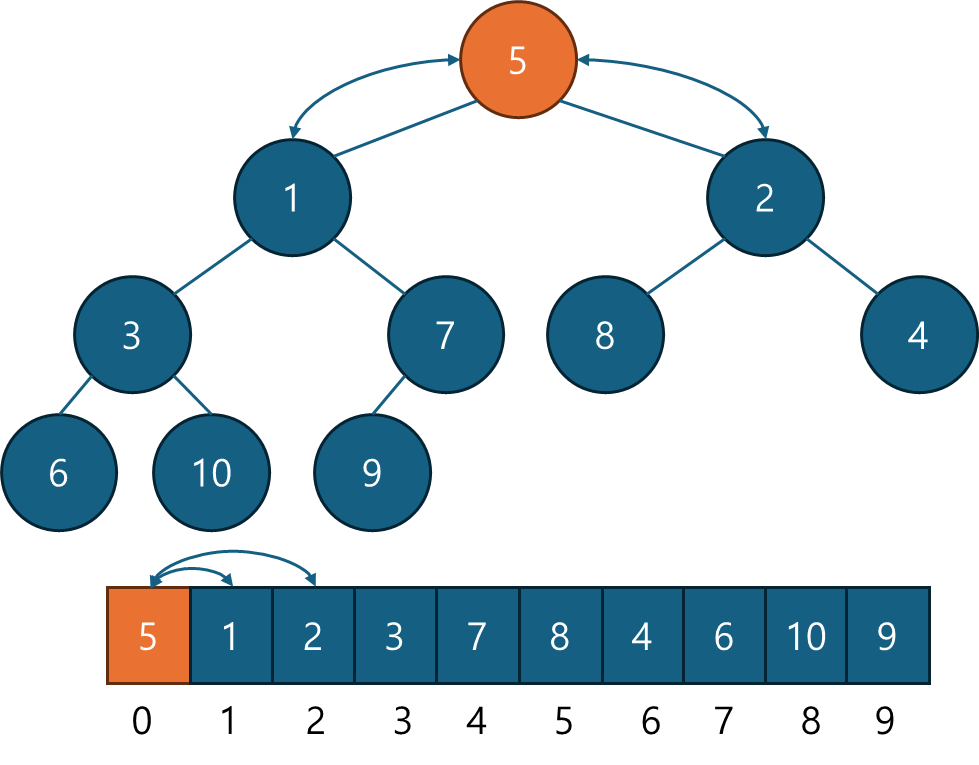



2. 루트 값을 결과에 저장하고 마지막 노드와 스왑, 힙 성질이 깨진 트리의 루트에 heapify를 적용해서 다시 힙구조를 만족시키도록 변경.






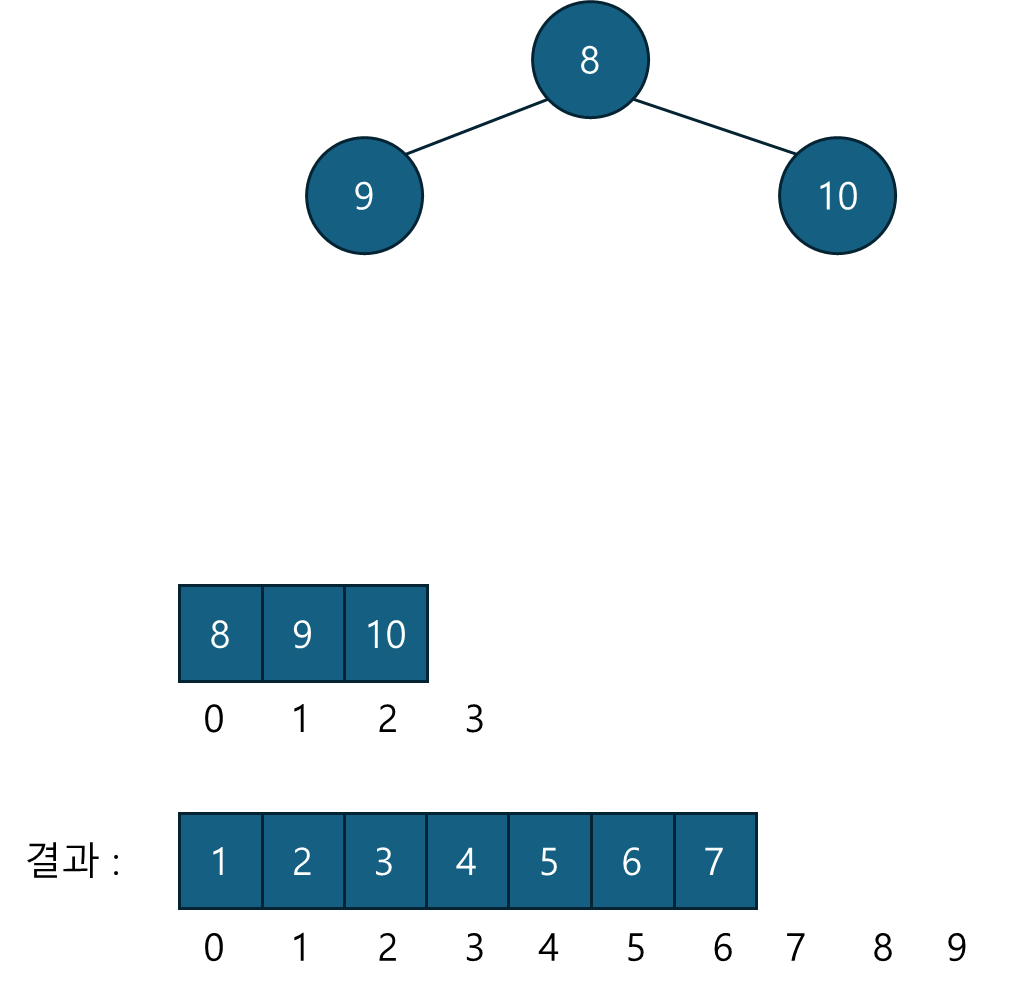



C++ 구현
벡터의 삭제 방법을 몰라서 벡터의 마지막을 실제로 삭제하는 대신 사용 범위를 제한하는 방식으로 구현했다. C++ 공부할 때 STL 사용 방법도 연습해야 할 것 같다.
#include <iostream>
#include <vector>
using std::vector;
void Heapify(vector<int>& _arr, int _size, int num)
{
// 인덱스를 0부터 시작하면 num번째의 왼쪽 자식은 2*num+1, 오른쪽 자식은 2*num+2
const int LEFT = 2 * num + 1;
const int RIGHT = 2 * num + 2;
// 자식 없는 경우는 리턴
if (_size - 1 < LEFT) // 자식 없음 = 마지막 인덱스보다 왼쪽 자식의 인덱스가 더 크면.
return;
if (RIGHT < _size) // 자식이 두 개라면 = 마지막 인덱스보다 오른쪽 자식의 인덱스가 작거나 같으면.
{
// 왼쪽이 더 작음
if (_arr[LEFT] < _arr[RIGHT])
{
// 내가 왼쪽 자식보다 크면
if (_arr[num] > _arr[LEFT])
{
// 나와 왼쪽 자식을 스왑
int temp = _arr[num];
_arr[num] = _arr[LEFT];
_arr[LEFT] = temp;
Heapify(_arr, _size, LEFT);
}
}
// 오른쪽이 더 작음
else
{
// 내가 오른쪽 자식보다 크면
if (_arr[num] > _arr[RIGHT])
{
// 나와 오른쪽 자식을 스왑
int temp = _arr[num];
_arr[num] = _arr[RIGHT];
_arr[RIGHT] = temp;
Heapify(_arr, _size, RIGHT);
}
}
}
else // 자식이 한 개라면 (왼쪽)
{
// 내가 왼쪽 자식보다 크면
if (_arr[num] > _arr[LEFT])
{
// 나와 왼쪽 자식을 스왑
int temp = _arr[num];
_arr[num] = _arr[LEFT];
_arr[LEFT] = temp;
Heapify(_arr, _size, LEFT);
}
}
}
void HeapSort(vector<int>& _arr)
{
vector<int> copyArr(_arr);
int mid = copyArr.size() / 2; // 내림
// 자식이 있는 노드에 대해서만 Heapify 진행 (거꾸로)
for (int i = mid - 1; i >= 0; --i)
{
Heapify(copyArr, copyArr.size(), i);
}
// 루트 값을 꺼내고, 맨 마지막과 스왑해서 삭제한 후 heapify하는 과정을 반복
// 실제로 삭제하는 대신 사용하는 배열의 범위를 줄여가는 것으로 구현함.
for (int i = 0; i < copyArr.size(); ++i)
{
// 루트 값을 꺼내서 원본 배열에 삽입
_arr[i] = copyArr[0];
// 루트에 맨 마지막 값을 대입
copyArr[0] = copyArr[copyArr.size() - i - 1];
Heapify(copyArr, copyArr.size() - i - 1, 0);
}
}
int main()
{
vector<int> arr = { 5,1,2,3,9,8,4,6,10,7 };
HeapSort(arr);
return 0;
}'알고리즘' 카테고리의 다른 글
| [알고리즘] 계수 정렬 (Counting Sort), O(N) (0) | 2024.09.07 |
|---|---|
| [알고리즘] 정렬 - 퀵 정렬, O(NlogN) (0) | 2024.03.17 |
| [알고리즘] 정렬 - 병합 정렬, O(NlogN) (0) | 2024.03.17 |
| [알고리즘] 정렬 - 삽입 정렬, O(N^2) (0) | 2024.03.17 |
| [알고리즘] 정렬 - 버블 정렬, O(N^2) (0) | 2024.03.17 |




